[ Triangulation ] Ear Clipping Algorithm 삼각기법 알고리즘

Ear Clipping 알고리즘은, 기존 Triangulation 알고리즘 중 가장 쉽고 널리 알려진 알고리즘이다

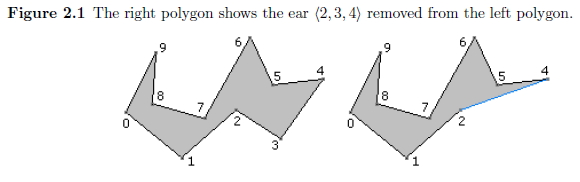
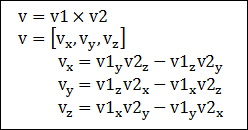http://www.geometrictools.com/Documentation/TriangulationByEarClipping.pdf

위 링크의 논문 참조 바란다.


논문을 바탕으로 정리를 하자면, 우선으로 다음과 같은 조건을 갖춰야한다.

1. Polygon line은 정렬 되어있어야 한다.
2. Polygon line 의 끝점과 시작점은 서로 만나야한다 ( Closed Curve )

다음과 같이 Simple 로 폴리곤이 정의 되어 있어야 한다.

폴리곤의 배열 순서는 다음과 같다.
P = [0,1,2,3,4,5,6,7,8,9]  (0과 9는 서로 만남)

삼각화를 하기전 데이타 분류작업이 선 진행 되어야 한다.

데이터는 다음과 같이 3가지 종류로 분류 된다.

1. reflex vertex
2. convex vertex
3. ear tip

reflex vertex는 P(i-1) 점과 P(i), P(i+1) 점을 잇는 각도가 시계방향으로 봣을때, 각이 180도보다 큰 각을 말한다.
reflex vertex는 P(i-1) 점과 P(i), P(i+1) 점을 잇는 각도가 시계방향으로 봣을때, 각이 180도보다 작은 각을 말한다.

ear tip은 P(i-1) 점과 P(i), P(i+1)으로 삼각형을 만들었을때, 삼각형 내에 다른 점들이 포함되지 않는 점의 모음이라고 할 수 있다.

예제 샘플에서의 분류는

C = {0,1,3,4,6,9}

R = {2,5,7,8}

E = {3,4,6,9} 

로 나눌 수 있다.

가장 먼저 해야 할 일은 Ear tip의 첫번째 상수인 P3을 제거 하는 일이다.
Ear tip 분류자체가 한점을 포함하지 않는 삼각형에 관한 점이기에 P3이 중심이되는 삼각형은 독립적으로 분류가 가능하다.

P3을 제거함으로써 ,P2와 P4가 변화를 갖게 되는데 첫번째 경우  P4는 convex값이다.

C = {0,1,3,4,6,9}

R = {2,5,7,8}

E = {4,6,9} 

그다음 Ear tip인 P4를 제거 한다.

P2는 여전히 Convex값을 가지지만 P5는 더이상 reflex값이 아니라 convex값으로 바뀐다.
relfex 리스트에서 P5는 제거 되고 ear list에 P5가 추가 된다.
C = {0,1,3,5,6,9}
R = {2,6,7,8}
E = {5,6,9} ( P4 제거 되고 P5 추가된 상태 )

변화에 따라 그다음 제거대상자인 P5를 제거한다.

P2가 reflex 였으나 이제 convex로 바뀌였다. 그러나 P2를 ear test 하였을경우 P7이 삼각형 안쪽으로 들어가므로, P2는 ear tip이 아니다.
R = {7,8} ( P2가 리스트에서 제거된 상태)
E = {6,9} ( P5가 제거된 상태 )

P6이 제거된 상태

 P2는 convex였으므로, 그대로 남는다. 하지만 Ear 그룹이 아니였음에도 불구하고, P6이 제거된 상황에서 재검을 하면 P2는 Ear그룹에 소속된다.
E = {9,2}

좀 이해안가는 문장이
The ear list is written this way because the new ear is added first before the old ear is removed. Before removing the old ear, it is still considered to be first in the list.

왜 ear list가 이렇게 배열 됬는지에 대해서, 이전 ear가 제거 되기 전에 새 ear가 먼저 추가 되어서라 한다. 이전 ear를 제거하기 전에 리스트내에 첫번째로 있어야할것이 아직 고려되기 때문이라 하지만, list 들을 훑다보면, 제거된 P6의 다음 은 7->8->9->0->1->2 이므로
9,2 순이 아닐까 한다.

아무튼 그다음 제거 대상 ear 인 P9를 제거한다.

P9이 제거된 상태

E = {0,2,8}

그다음 대상자인 0, 2,8 순으로 ear list 가 변경이 된다.

P0이 제거된 상태

E = {2,8}

P2가 제거된 상태

완성 상태! 

Vector 기본

항상 계산하던 벡터 개념이지만 늘 다시보려면 책을 보게된다
언제쯤 안까먹을지 -_-

1. Vector 란, 크기와 방향을 나타내는 수학적도구.
Vector3 v = [Vx,Vy,Vz] 로 구성된다.

2, Vector 의 성분 계산
V = B - A
V = (Bx, By, Bz) - ( Ax, Ay, Az)
V = (Bx - Ax), (By - Ay), (Bz - Az)
ex) Vector3 V = new Vector(Bx-Ax, By-Ay, Bz-Az);

3. Vector의 크기
벡터의 크기는 벡터의 화살표 길이다.
피타고리스 정리에 의해 "X값의 제곱 + Y값을 제곱 = (벡터의 크기)의 제곱"  공식
ex) float length = sqrt(x*x + y*y + z*z );

4. 단위벡터
방향만을 나타내는 벡터이며, 크기는 1이다
기존 벡터를 단위벡터로 만드는것을 정규화(Normalization)라고 한다.
기존의 벡터를 자신의 크기로 나누어주면 된다.
ex) Vector3 N = new Vector(x/length, y/length, z/length);

5, 벡터의 내적(각도) - 보통은 각도를 알기위해 쓰죠-
벡터의 곱셈은 내적과 외적으로 정의되며, 내적값은 스칼라값이다.
벡터A와 벡터B의 내적을 구하면 두 벡터가 이루는 각도가 나온다.

크기가 같은 두 벡터라 할지라도 두벡터사이에 각도에 따라 내적(크기)는 달라진다.

각 벡터의 성분간의 곱을 모두 더하면 벡터 A와 B의 내적이 나온다
ex) float dot = Ax*Bx + Ay*By + Az*Bz;

같은 벡터의 내적은 길이의 제곱이다.
ex) A.dot(A) == A.length * A.length

http://blog.naver.com/gt7461?Redirect=Log&logNo=110155953363

내적이 0이면 두벡터는 서로 직교한다 ( 법선벡터, Normal Vector 노멀벡터)
내적이 양수이면 두 벡터의 사잇각은 0 ~ 180도 사이다.
내적이 음수면 두 벡터의 사잇각은 180을 넘는다 ( 뒷면 판단시 사용 )

http://en.wikipedia.org/wiki/Dot_product

6. 벡터의 외적
두 벡터에 모두 수직한 벡터 ( 노멀벡터)를 값으로 가진다
AXB로 표현되는데, 교환법칙이 성립하지 않으므로, 순서에 주의

AXB = [A2B3 - A3B2, A3B1 - A1B3, A1B2 - A2B1]
ex) Vector3 Cross = new Vector( a.y*b.z - a.z*b.y, a.z*b.x - a.x*bz, a.x*b.y - a.y*bx )

http://en.wikipedia.org/wiki/Cross_product

STL File - Volume 구하기

아- 넘 졸리다..

얼마전 STL Vector정보가 3 Points 에대한 Vector 정보가 아닌, 쉐이딩 정보라는것을 Wiki 에서 발견했다.. -_-

나름 Grading 한 정보가 Vector 정보가 맞지 않아 고심했던 걸 생각하면 괴씸하군. 뒤통수 맞은 기분 ㅠㅠ

쉐이딩 정보를 어떻게 변환해야할지에 대해서는 아직 고심하지 않았지만,
볼륨을 구하는 목적의 프로그램에는 특별히 상관이 없어서 나중에 검토 하기로 했다.



Let we have field F(P)=P . It have constant divergence Ñ·F = 3 . Flow of F(P) through triangle ABC is 1/2 * A.BXC . Method above uses exactly that. (it indeed could be said that it just adds volume of pyramids. [grin] but you can derive it from divergence theorem (aka Gauss's Theorem) , and will not have problems proving that negative volume trick will work)

(2everyone who suggested my method explained in other tread, that only differs in "volume+=(v0.x+v1.x+v2.x)*Cross(v1-v0,v2-v0).x" (uses field F(P)=[P.x,0,0] with divergence 1) : it was made to simplify computation of volume of submerged object. In other cases, "pyramids method" is nicer)
       
Suppose you have a vertex array V[] of N vertices. The triangle list is an array I[] of 3*T indices into the vertex array and represents T triangles. Suppose the mesh is closed, each edge is shared by two triangles, and the mesh is not self-intersecting ("water tight" in the vernacular). Also assume that the triangles are counterclockwise oriented as viewed by an observer outside the mesh. Finally, assume that the mass density is constant (1). If nonconstant, the problem is much more difficult.

float volume = 0;
int* index = I;
for (i = 0; i < T; i++)
{
    Vector3 v0 = V[*index++];
    Vector3 v1 = V[*index++];
    Vector3 v2 = V[*index++];
    volume += Dot(v0,Cross(v1,v2));
}
volume /= 6;

세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기)

p(0,0,0), Q(2,4,6), R(-1,2,7)
이 세점으로 만들어지는 평면에 법선벡터 구하기.

P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는
벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다.
따라서 벡터 PQ와 벡터 PR 의 외적(크로스곱)을 구하면 됩니다.

벡터 PQ = Q - P = (2,4,6) - (0,0,0) = (2,4,6)
벡터 PR = R - P = (-1,2,7) - (0,0,0) = (-1,2,7)

(벡터 PQ) × (벡터 PR)
= (2,4,6) × (-1,2,7)
= (4 * 7 - 6 * 2)i - {2 * 7 - 6 * (-1)}j + {2 * 2 - 4 * (-1)}k
= 16i - 20j + 8k
= (16, -20, 8)

따라서 주어진 평면에 법선벡터는 (16, -20, 8) 입니다. 간단히 나타내려면 4를 나누어
(4, -5, 2) 라고 해도 무방합니다. (벡터의 실수배는 평행한 벡터이므로)


외적 구하는 법