항상 계산하던 벡터 개념이지만 늘 다시보려면 책을 보게된다
언제쯤 안까먹을지 -_-
1. Vector 란, 크기와 방향을 나타내는 수학적도구.
Vector3 v = [Vx,Vy,Vz] 로 구성된다.
2, Vector 의 성분 계산
V = B - A
V = (Bx, By, Bz) - ( Ax, Ay, Az)
V = (Bx - Ax), (By - Ay), (Bz - Az)
ex) Vector3 V = new Vector(Bx-Ax, By-Ay, Bz-Az);
3. Vector의 크기
벡터의 크기는 벡터의 화살표 길이다.
피타고리스 정리에 의해 "X값의 제곱 + Y값을 제곱 = (벡터의 크기)의 제곱" 공식
ex) float length = sqrt(x*x + y*y + z*z );
4. 단위벡터
방향만을 나타내는 벡터이며, 크기는 1이다
기존 벡터를 단위벡터로 만드는것을 정규화(Normalization)라고 한다.
기존의 벡터를 자신의 크기로 나누어주면 된다.
ex) Vector3 N = new Vector(x/length, y/length, z/length);
5, 벡터의 내적(각도) - 보통은 각도를 알기위해 쓰죠-
벡터의 곱셈은 내적과 외적으로 정의되며, 내적값은 스칼라값이다.
벡터A와 벡터B의 내적을 구하면 두 벡터가 이루는 각도가 나온다.
크기가 같은 두 벡터라 할지라도 두벡터사이에 각도에 따라 내적(크기)는 달라진다.
각 벡터의 성분간의 곱을 모두 더하면 벡터 A와 B의 내적이 나온다
ex) float dot = Ax*Bx + Ay*By + Az*Bz;
같은 벡터의 내적은 길이의 제곱이다.
ex) A.dot(A) == A.length * A.length
내적이 0이면 두벡터는 서로 직교한다 ( 법선벡터, Normal Vector 노멀벡터)
내적이 양수이면 두 벡터의 사잇각은 0 ~ 180도 사이다.
내적이 음수면 두 벡터의 사잇각은 180을 넘는다 ( 뒷면 판단시 사용 )
http://en.wikipedia.org/wiki/Dot_product
6. 벡터의 외적
두 벡터에 모두 수직한 벡터 ( 노멀벡터)를 값으로 가진다
AXB로 표현되는데, 교환법칙이 성립하지 않으므로, 순서에 주의
AXB = [A2B3 - A3B2, A3B1 - A1B3, A1B2 - A2B1]
ex) Vector3 Cross = new Vector( a.y*b.z - a.z*b.y, a.z*b.x - a.x*bz, a.x*b.y - a.y*bx )
http://en.wikipedia.org/wiki/Cross_product
2013년 6월 11일 화요일
STL File - Volume 구하기
아- 넘 졸리다..
얼마전 STL Vector정보가 3 Points 에대한 Vector 정보가 아닌, 쉐이딩 정보라는것을 Wiki 에서 발견했다.. -_-
나름 Grading 한 정보가 Vector 정보가 맞지 않아 고심했던 걸 생각하면 괴씸하군. 뒤통수 맞은 기분 ㅠㅠ
쉐이딩 정보를 어떻게 변환해야할지에 대해서는 아직 고심하지 않았지만,
볼륨을 구하는 목적의 프로그램에는 특별히 상관이 없어서 나중에 검토 하기로 했다.
Let we have field F(P)=P . It have constant divergence Ñ·F = 3 . Flow of F(P) through triangle ABC is 1/2 * A.BXC . Method above uses exactly that. (it indeed could be said that it just adds volume of pyramids. [grin] but you can derive it from divergence theorem (aka Gauss's Theorem) , and will not have problems proving that negative volume trick will work)
(2everyone who suggested my method explained in other tread, that only differs in "volume+=(v0.x+v1.x+v2.x)*Cross(v1-v0,v2-v0).x" (uses field F(P)=[P.x,0,0] with divergence 1) : it was made to simplify computation of volume of submerged object. In other cases, "pyramids method" is nicer)
Suppose you have a vertex array V[] of N vertices. The triangle list is an array I[] of 3*T indices into the vertex array and represents T triangles. Suppose the mesh is closed, each edge is shared by two triangles, and the mesh is not self-intersecting ("water tight" in the vernacular). Also assume that the triangles are counterclockwise oriented as viewed by an observer outside the mesh. Finally, assume that the mass density is constant (1). If nonconstant, the problem is much more difficult.
얼마전 STL Vector정보가 3 Points 에대한 Vector 정보가 아닌, 쉐이딩 정보라는것을 Wiki 에서 발견했다.. -_-
나름 Grading 한 정보가 Vector 정보가 맞지 않아 고심했던 걸 생각하면 괴씸하군. 뒤통수 맞은 기분 ㅠㅠ
쉐이딩 정보를 어떻게 변환해야할지에 대해서는 아직 고심하지 않았지만,
볼륨을 구하는 목적의 프로그램에는 특별히 상관이 없어서 나중에 검토 하기로 했다.
Let we have field F(P)=P . It have constant divergence Ñ·F = 3 . Flow of F(P) through triangle ABC is 1/2 * A.BXC . Method above uses exactly that. (it indeed could be said that it just adds volume of pyramids. [grin] but you can derive it from divergence theorem (aka Gauss's Theorem) , and will not have problems proving that negative volume trick will work)
(2everyone who suggested my method explained in other tread, that only differs in "volume+=(v0.x+v1.x+v2.x)*Cross(v1-v0,v2-v0).x" (uses field F(P)=[P.x,0,0] with divergence 1) : it was made to simplify computation of volume of submerged object. In other cases, "pyramids method" is nicer)
Suppose you have a vertex array V[] of N vertices. The triangle list is an array I[] of 3*T indices into the vertex array and represents T triangles. Suppose the mesh is closed, each edge is shared by two triangles, and the mesh is not self-intersecting ("water tight" in the vernacular). Also assume that the triangles are counterclockwise oriented as viewed by an observer outside the mesh. Finally, assume that the mass density is constant (1). If nonconstant, the problem is much more difficult.
float volume = 0;
int* index = I;
for (i = 0; i < T; i++)
{
Vector3 v0 = V[*index++];
Vector3 v1 = V[*index++];
Vector3 v2 = V[*index++];
volume += Dot(v0,Cross(v1,v2));
}
volume /= 6;
2013년 6월 6일 목요일
세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기)
p(0,0,0), Q(2,4,6), R(-1,2,7)
이 세점으로 만들어지는 평면에 법선벡터 구하기.
P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는
벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다.
따라서 벡터 PQ와 벡터 PR 의 외적(크로스곱)을 구하면 됩니다.
벡터 PQ = Q - P = (2,4,6) - (0,0,0) = (2,4,6)
벡터 PR = R - P = (-1,2,7) - (0,0,0) = (-1,2,7)
(벡터 PQ) × (벡터 PR)
= (2,4,6) × (-1,2,7)
= (4 * 7 - 6 * 2)i - {2 * 7 - 6 * (-1)}j + {2 * 2 - 4 * (-1)}k
= 16i - 20j + 8k
= (16, -20, 8)
따라서 주어진 평면에 법선벡터는 (16, -20, 8) 입니다. 간단히 나타내려면 4를 나누어
(4, -5, 2) 라고 해도 무방합니다. (벡터의 실수배는 평행한 벡터이므로)
외적 구하는 법
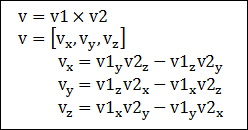
이 세점으로 만들어지는 평면에 법선벡터 구하기.
P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는
벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다.
따라서 벡터 PQ와 벡터 PR 의 외적(크로스곱)을 구하면 됩니다.
벡터 PQ = Q - P = (2,4,6) - (0,0,0) = (2,4,6)
벡터 PR = R - P = (-1,2,7) - (0,0,0) = (-1,2,7)
(벡터 PQ) × (벡터 PR)
= (2,4,6) × (-1,2,7)
= (4 * 7 - 6 * 2)i - {2 * 7 - 6 * (-1)}j + {2 * 2 - 4 * (-1)}k
= 16i - 20j + 8k
= (16, -20, 8)
따라서 주어진 평면에 법선벡터는 (16, -20, 8) 입니다. 간단히 나타내려면 4를 나누어
(4, -5, 2) 라고 해도 무방합니다. (벡터의 실수배는 평행한 벡터이므로)
외적 구하는 법
피드 구독하기:
덧글 (Atom)

